Es gibt viele ungelöste Fragen zum Problem, wie sich die menschliche Fähigkeit zum Zählen herausgebildet hat. Zu Beginn dürfte die Fähigkeit gestanden haben, Anzahlen konkreter Gegenstände als gleich oder als unterschiedlich zu erfassen. Knochen mit Einkerbungen, die Mengenangaben darstellen, sind seit dem Jungpaläolithikum belegt. Auch die Orientierung in Zeit und Raum, z.B. zur Jagd und Nahrungssuche, erfordert “geometrische“ Grundvorstellungen, ebenso die Herstellung keramischer Erzeugnisse, Waffen und Werkzeugen oder der Bau von Gräbern, Behausungen etc. Geometrische Muster finden sich schon früh als Dekor auf Keramik wieder.

Fig. 1: (a) Ishango-Knochen mit Einkerbungen, Zentralafrika, ca. 20.000 v.Chr.(?). (b) Dekorierte Keramik (Naqada II, Mitte 4. Jtd. v.Chr.). (c) Anhängetäfelchen mit Zahlen aus dem Grab U-j, Abydos, Umm el-Qaab, um 3350 v. Chr.

Im Laufe der frühdynastischen Zeit, mit der Herausbildung des Zentralstaates, entstand die Notwendigkeit, Vorgänge in Wirtschaft und Verwaltung schriftlich festzuhalten; die Hieroglyphenschrift entwickelte sich. Gleichzeitig mit den ersten niedergeschriebenen Worten sind auch Zahlzeichen nachweisbar, die ein Dezimalsystem (ohne Null und ohne Positionswertbeschreibungen) belegen. Für die Zahlenwerte 1, 10, 100, 1000, 10.000, 100.000 und 1.000.000 gab es jeweils ein eigenes Zeichen, die ggf. additiv zusammengesetzt sind. Rationale Zahlen werden als Stammbrüche, die ggf. ebenfalls addiert werden, wiedergegeben.

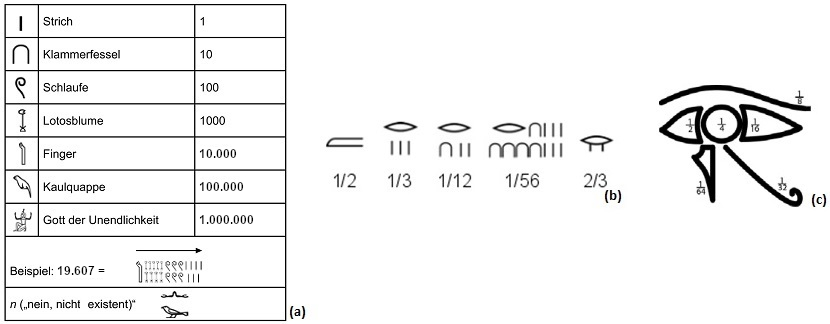
Fig. 2: Übersicht über das Zahlenspektrum: (a) Natürliche Zahlen, (b) Stammbrüche, (c) Brüche bei der Maßangabe Hekat

Rückschlüsse über das mathematische Verständnis der Alten Ägypter geben zum einen die pure Präsenz von Zahlen wie auf den Anhängetäfelchen aus U-j, zum anderen kulturtechnische Übertragung zwischen Wissens- und Handlungsbereichen und vor allem Texte über Mathematik. In ihnen zeigt sich, dass das mathematische Wissen ganz pragmatisch an die realen administrativ-ökonomischen Bedingungen gekoppelt ist.

Gelehrt wurde mathematisches Wissen vermutlich im Rahmen der Schreiberausbildung. Für viele Beamte in der Administration gehörten Zählen, (Ver)Messen und Berechnen von Flächen und Volumina zur Arbeit. Im Papyrus Anastasi V, der dem Schulkontext zuzurechnen ist, heißt es:

„Was Folgendes betrifft: Ich habe Dich zur Schule geschickt (…), um Dich für dieses bedeutende Amt zu unterrichten. (…) Sie (sagen): 3 und 3. (…). Du wirst Berechnungen formulieren, indem du still bist. Laß nicht zu, daß ein Laut gehört wird! Sei verschlossen(?) mit deinem Mund! (…). Folge den Plänen deines Lehrers. Höre seine Lehre, werde ein Schreiber!“ (pAn V, 22:6ff., Neues Reich)

Im Papyrus Anastasi I (dem sogenannten satirischen Brief des Hori) werden bespielhaft verschiedene mathematische Aufgabenstellungen gegeben, die dem administrativen Alltag der Beamten zuzuordnen sind:

„Eine Rampe von 730 Ellen Länge und 55 Ellen Breite soll gebaut werden, mit 120 Hohlräumen, ausgelegt mit Schilfrohr und Balken, mit einer Höhe von 60 Ellen an ihrer Spitze, von 30 Ellen in ihrer Mitte, mit einer Böschung von 15 Ellen, mit ihrem Fundament von 5 Ellen (Stärke). (…) Beantworte uns ihren Ziegelbedarf! Siehe doch, ihre Maße sind vor dir, ein jeder ihrer Hohlräume beträgt 30 Ellen (Länge) und 7 Ellen (Breite).
(…)
Du wirst nach Djahi gesandt mit einem Auftrag an der Spitze des siegreichen Heeres … Die Truppen des Heeres, die vor dir sind, betragen 1900 Mann, die Scherden 620, die Qahag 1600, die Meschwesch (…) die Nubier 880; zusammen 5000. (…) Den Anteil eines jeden Mannes (Ration) in sein Hand.“ (pAn I, 14:2ff, Neues Reich)

Texte über Mathematik sind in einiger Anzahl seit dem Mittleren Reich überliefert: pMoskau E 4676, Mathematische Lederrolle BM EA 10250, Fragmente aus Lahun, pBerlin 6619, Kairener Holztafeln CG 25367–8 (Mittleres Reich), pRhind BM EA10058 (2. Zwischenzeit), Ostrakon Senmut 153, Ostrakon Turin 57170 (Neues Reich), pCairo JE 89127–30; 89137–43, pBM 10399, 10520, 10794, pCarlsberg 30 (Spätzeit–griechisch-römische Zeit). Die dort gestellten Aufgaben stehen beispielhaft für mathematische Problemstellungen und deren Lösungswege. Sie lassen sich drei größeren Gruppen zuordnen:

Übung mathematischer Grundtechniken

• skm-Aufgaben (Addition & Subtraktion von Brüchen)
• ꜥḥꜥ-Aufgaben (Bestimmung einer Menge, bei gegebener Summe einer Menge X und eines Bruchteils oder Vielfaches von ihr)
• Metrologische ꜥḥꜥ-Aufgaben (zu den arithmetischen Operationen zusätzlich metrologische Kenntnisse)
• ꜣḥ.t-Aufgaben (Berechnung von (Felder-)Flächen)

administrative Mathematik

• Rationenberechnung
• psw-Aufgaben (Berechnung der Anzahl Bier oder Brot aus einer gegebenen Menge Getreide)
• bꜣkw-Aufgaben (Berechnung von Abgaben einzelner Berufsgruppen)
• Speicherberechnungen (Volumenberechnung von Speichern)

Berechnung von Konstruktionselementen

• sqd-Aufgaben (Zusammenhang zwischen Grundseite, Höhe, Breite einer Pyramide oder Pfeilers)
• Berechnung von Schiffsteilen

Die bisher bekannten Mathematikaufgaben zeigen den Stellwert, den das Lösen mathematischer Probleme im administrativen Alltag einnahm. Es ist anzunehmen, dass die ägyptische Mathematik Einfluss auf die Etablierung der Mathematik als Wissenschaft in der hellenistischen Welt ausübte. So überliefert Herodot, dass die Griechen die Geometrie von den Ägyptern und die Astronomie von den Babyloniern übernahmen.