Mathematics
There are many open questions about how the human ability to count has evolved in the past. This cognitive development might have begun with the ability to identify numbers of specific objects as being the same or different. Bones with incisions marking quantities are known from the Upper Palaeolithic onwards. Furthermore, orientation in time and space, for example, while hunting or searching for food, requires basic geometrical knowledge; and the same applies to the production of pottery, weapons and tools, or the construction of tombs and buildings etc. Thus, geometric patterns have been found as early as decoration on pottery.

Fig. 1: (a) Ishango-bone with incisions, Central Africa, about 20,000 BC (?) (b) Decorated pottery (Naqada II) (c) Labels with numbers from the tomb U-j (Abydos, Umm el-Qaab)
The formation of a centralized state in Egypt during the Early Dynastic Period required an increasing necessity to record processes in economy and administration. This was one of the most important factors for developing (hieroglyphic) writing. Representations of numbers appeared at the same time, which indicate a decimal system without zero and without positional (place-value) notation. Seven distinct hieroglyphic signs represented the powers of 10 (from 1 to 1,000,000), wherein each of these signs was written as often as required to represent the actual number. Rational numbers were noted as fractions, which may also be added together.
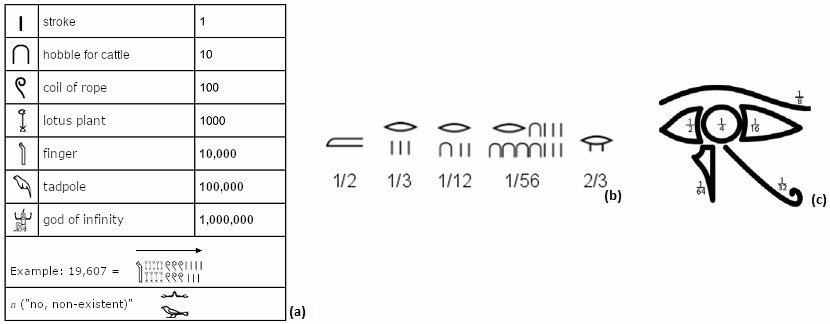
Fig. 2: Overview of the ancient Egyptian numerical system: (a) Natural numbers (b) Fractions (c) Fractions within the metrological system Hekat (standard unit for measuring cereals)
Conclusions about ancient Egyptian mathematics can be drawn from the presence of numbers, like on the labels from the tomb U-j, from cultural-technical transfer between areas of knowledge and practice, and above all from the corpus of mathematical texts. These show that mathematical knowledge was pragmatically linked to real administrative and economic conditions.
As literacy and numeracy were strongly connected, mathematical practice was a comprehensive part of the education of a (professional) scribe. Daily practices of an official in administration included counting, measuring and calculating area and volume, as is described in papyrus Anastasi V, which is attributed to a didactic context:
“I have placed you at the school (...) in order to instruct and to teach you concerning this aggrandizing calling. (...) They (say): ‘Three plus three’. (...) You will make calculations quietly: let no sound [coming forth (?)] from your mouth be heard. (...) Fall in with the ways of your instructor and hear his teachings. Be a scribe. (...)“ (pAn V, 22:6–23,7, New Kingdom; Caminos, LEM, 262–263).
Papyrus Anastasi I (the so-called Satirical Letter of a scribe named Hori) includes several examples of mathematical problems relating to the everyday administrative challenges of officials:
“A ramp shall be made of (length) 739 cubits, width 55 cubits, with 120 compartments, filled with reeds and beams. For height: 60 cubits at its top to 30 cubits in its middle, and an inclination of 15 cubits, its base 5 cubits. (...) Answer for us its need of bricks. Look, its measurements are before you. Each one of its compartments is of 30 cubits (in length) and a width of 7 cubits.” (pAn I, 13,8–14,8, New Kingdom; Imhausen, Mathematics in Ancient Egypt, 151).
Further issues addressed in the letter concern, for example, the transport of an obelisk, the calculation of rations for an expedition and the erection of a colossal monument.
Mathematical texts have been preserved from the Middle Kingdom to the Graeco-Roman Period. They present mathematical problems and their solutions by means of examples, which, according A. Imhausen (Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Ägyptologische Abhandlungen 65, Wiesbaden 2003), can be assigned to three larger groups:
(1) Mathematical basics
- skm-problem (addition and subtraction of fractions)
- ꜥḥꜥ-problem (determination of an unknown quantity from a given relation)
- Metrological ꜥḥꜥ-problem (arithmetic procedures in combination with metrological knowledge)
- ꜣḥ.t-problem (calculation of (agricultural) areas)
(2) Administrative mathematics/practical problems
- Calculations of rations
- psw-problem (mathematical framework in order to assess production of bread and beer from grain)
- bꜣkw-problem (calculating the produce of different professions)
- Determination of the content of a granary (calculation of volume)
(3) Mathematics relating to architecture and construction
- sqd-problem (problems related to base, height, and inclination of pyramids or pillars)
- Calculation for the parts of ships
The practical background of the problems, as documented in the sources, demonstrates that mathematical procedures must have played an increasingly vital role in education and the daily administrative routine of a scribe.
Herodotus wrote that geometry was invented in Egypt and then passed into Greece. Therefore, in this respect, Egyptian mathematics may well have had an impact on the development of mathematics as a science in the Hellenistic world.
